算法

Table of Contents

List of Tables

1 常规算法

1.1 排序

1.1.1 快速排序

快速排序是冒泡排序的改进版，其思想是选定待排序数据中的一个值作为比较轴，然 后将待排序数据与该值比较，将他们分配到轴两端，其中左边的比轴小，右边的比轴 大，循环的在左右两边的数据做快速排序操作，直到最后排序完毕。

1.2 最优化

许多实际问题利用数学建模的方法得到下面常规的优化形式：\(min f(x), x\in{D}\), 其中x是n维矢量，D是问题的定义域，F是可行域。关于f(x)

  1. 当\(x=(x)\)时，f(x)是一条曲线；
  2. 当\(x=(x_{1}, x_{2})\)时，\(f(x_{1}, x_{2})\)是一个曲面；
  3. 当\(x=(x_{1}, x_{2}, x_{3})\)时，\(f(x_{1}, x_{2}, x_{3})\)是一个体密度；
  4. 当\(x=(x_{1}, x_{i}..., x_{n})\)时，\(f(x_{1}, x_{2}..., x_{n})\)是一个 超曲面；

所以，(超)曲面，就有对多极值，并且有一个全局最大值和全局最小值。有些算法， 只能在自己的小范围内搜索极大值和极小值，称为局部优化算法，也叫经典优化算法； 有些算法，可以搜索整个(超)曲面取值范围内搜索最大值或最小值，称为全局性优化 算法，也叫现代优化算法。最优化问题，一般分几种。

  • 无约束优化问题：就是在没有任何约束条件的情况下，求函数的最优解。通常表示 为\(min(f(x))\);
  • 等式约束优化问题: 通常给出若干个用等式表示的约束条件，然后在这些条件下， 求函数的最优解,通常条件表示为\(h_{i}(x)=0, i=1, ..., n\);
  • 不等式约束优化问题: 通常给出的约束条件有等式约束条件也有不等式约束条件， 不等式约束条件表示为\(g_{j}(x)<=0, j=1, ..., n\);

1.2.1 梯度下降法

梯度下降法属于无约束优化问题。

optimize1.png

见图\ref{img-optimize-example1}所示，局部极小值C点x0, 梯度，即导数，但是有 方向，是一个矢量，曲线情况下，表达式如下 \[f^{'}(x)=\frac{\mathrm{d}y}{\mathrm{d}x}\] 如果，\(f^{'}(x) > 0\)则x增加，y增加，相当于B点；如果\(f^{'}(x)<0\)则x增加， y减小，相当于A点。要搜索极小值C点，在A点必须向x增加方向搜索，此时与A点梯度 方向相反；在B点必须向x减小小方向搜索，此时与B点梯度方向相反。总之，搜索极小 值，必须向负梯度方向搜索。 梯度下降法原理：由高数知任一点的负梯度方向是函数值在该点下降最快的方向，则 利用负梯度作为极值搜索方向，达到搜寻区间最速下降的目的。而由极值点导数性质， 知道该点的梯度等于0，故而其终止条件也就是梯度逼近于0，也就是当搜寻区间非常 逼近极值点时，即当如下成立时，f(a)就是寻找到的f(x)的极值，该方法是一种局部 搜寻法。 \[\bigtriangledown{f(a)\rightarrow{0}}\] 求解函数在限制域下的极值 \[\min{f(x)},f\in{C}\] 计算步骤如下, 拿y=f(x)来类比

  1. 首先设定搜寻的初值(x0, y0), 学习率ε;
  2. 计算梯度y'=f'(x);
  3. 计算旧值(x0, y0)处的梯度值(x0', y0');
  4. 通过学习率计算新的x1, x1=x0+ε*x0';
  5. 通过x1计算新的y1, 完成一次更新返回3计算该点的梯度；
  6. 在(x, y)不断更新的过程中，需要有终止条件；

例1:函数\(y=\frac{x^{2}}{2}-2x\), 其图形见\ref{img-optimize-example2}, 计算 过程如下，由于选用的2个参数值没有取好，会导致来回震荡，在极值点附近反复搜索。

  1. 先给定2个参数\(\epsilon=1.5, \eta=0.01\);
  2. 计算导数\(\frac{\mathrm{d}y}{\mathrm{d}x} = x-2\);
  3. 计算当前导数值y' = -6;
  4. 修改当前参数\(x_{0}=-4->x_{1}=x_{0}-\epsilon*y'=-4-1.5*(-6)=5.0\)
  5. 计算当前导数值y'=3.0;
  6. 修改当前参数\(x_{1}=5.0->x_{2}=5.0-1.5*(3.0)=0.5\);
  7. 计算当前导数值y'=-1.5;
  8. ……

optimize2.png

例2：用梯度下降法求\(f(x_{1}, x_{2})=x_{1}^{2}+4x_{2}^{2}\)的极小值。

  1. 设初始点\(x^{(0)}=(1, 1)^{T}\);
  2. f梯度：\(\bigtriangledown{f(x_{1}, x_{2})}=(2x_{1}, 8x_{2})^{T}\);
  3. 由初始点得此点梯度值：\(\bigtriangledown{f(x^{(0)})}=(2, 8)^{T}\);
  4. 模：\(||\bigtriangledown{f(x^{(0)})}||=8.24621\);
  5. 第3步得负梯度：\(d^{(0)}=(-2, -8)^{T}\);
  6. 计算最佳步长：\(\min{f(x^{(0)}+s_{0}*d^{(0)})}=\min{(1-2s_{0})^{2}+4(1-8s_{0})^{2}}\);
  7. 得\(s_{0}=\frac{68}{520}\);
  8. 新点：\(x^{(1)}=(1, 1)^{T}-s_{0}(2, 8)^{T}=(0.738, -0.046)^{T}\), 返回3;

1.2.2 共轭梯度法

共轭梯度法也属于无约束优化问题。 对于多元二次方程 \[f(x)=\frac{X^{T}AX}{2}+B^{T}X+C\] 求导得 \[f'(x)=AX+B\] 因为针对X为向量，\[X^{T}AX\] 对X求导得\[2AX\] , \[B^{T}X\] 求导得B；

1.2.3 拉格朗日乘子法

一般无约束优化问题f(x)，只需要求f的各个偏导数，并令其等于0，就可以解出所需 要的极值，但是如果参入了约束条件，则不能这样做。然而拉格朗日乘子法可以将约 束条件融合进去使之成为一个类似无约束的优化问题，如此就可以比较方便的解决问 题。欲求n元函数\(f(x_{1}, x_{2}, ..., x_{n})\)在如下m个约束条件(m<n). $$

\begin{cases} y_{1}{x_{1}, x_{2}, ..., x_{n}} &= 0\\ y_{2}{x_{1}, x_{2}, ..., x_{n}} &= 0\\ ...\\ y_{m}{x_{1}, x_{2}, ..., x_{n}} &= 0\\ \end{cases}

\[ 拉格朗日方法是以\(1, C_{1}, C_{2}, ..., C_{m}\)这些未知常数顺次乘以\(f, y_{1}, y_{2}...\)并把它们加起来，得到新的函数F，即 \]F(x1,…, xn)=f(x1, …, xn)+C1y1(x1…xn)+…\[ 注意到约束条件的各个函数都是0，所以新函数F达到极值与原函数f达到极值时自变量 的值是相同的。函数F既然是各个x的函数，它达到极值时必然是对各个自变量x的偏微 分分别等于0.这样，求多个偏微分以后就得到n个新的方程。 \]

\begin{cases} \frac{\partial{f}}{\partial{x_{1}}}+C_{1}\frac{\partial{y_{1}}}{\partial{x_{1}}}+...C_{m}\frac{\partial{y_{m}}}{\partial{x_{1}}}=0\\ ...\\ \frac{\partial{f}}{\partial{x_{n}}}+C_{1}\frac{\partial{y_{1}}}{\partial{x_{n}}}+...C_{m}\frac{\partial{y_{m}}}{\partial{x_{n}}}=0\\ \end{cases}

$$ 显然，这n个方程式已经巧妙的把约束条件融合到求解的要求中。上面n个方程再加上 约束条件的m个方程式，就可以解出n+m个未知数，即n个x，m个C。这样就得到了这个 函数达到极值时的各自变量x的值，可以看到约束条件不同，得到的各个x值也不同。

1.2.4 拉格朗日对偶

某些条件下，把原始的约束问题通过拉格朗日函数转化为无约束问题，如果原始问题 求解棘手，在满足KKT的条件下用求解对偶问题来代替求解原始问题，使得问题求解更 加容易。

1.2.4.1 原始问题

假设\(f(x), c_{i}(x), h_{j}(x)\)是定义在\(R^{n}\)上的连续可微函数，要解决如 下的约束优化问题。 $$

\begin{cases} \min\limits_{x\in{R^{n}}} f(x) \\ s.t. & c_{i}(x)=0, i=1, ..., k\\ & h_{j}(x)<=0, j=1, ..., l\\ \end{cases}

\[ 如果不考虑约束条件，原始问题就是 \]min\limitsx∈{Rn}f(x)$$ 因为假设其是连续可微，对f(x)求导，然后令导数为0，就可解出最优解。然而现在是 有约束条件，考虑想办法把约束条件去掉就好了，拉格朗日函数正是用于解决此问题。

1.2.4.2 广义拉格朗日函数

一般意义下的拉格朗日函数如下 \[ L(x, \alpha, \beta)=f(x)+ \sum_{i=1}^{k}\alpha_{i}c_{i}(x)+\sum_{j=1}^{l}\beta_{j}h_{j}(x) \] \(\alpha_{i},\beta_{j}\)也就是拉格朗日乘子，其中\(\alpha_{i}\geq 0). 现在，如果把\(L(x, \alpha, \beta)\)看作关于\(\alpha_{i}, \beta_{j}\)的函数， 要求其最大值，即 \[\max\limits_{\alpha, \beta:\alpha_{i}\geq 0}L(x, \alpha, \beta) \] 再次注意\(L(x, \alpha, \beta)\)是一个关于\(\alpha_{i}, \beta_{j}\)的函数， 假设求得\(L(x, \alpha, \beta)\)的最大值时的\(\alpha_{i}, \beta_{j}\)，即 \(\alpha_{i}, \beta_{j}\) 此时已经是确定值，则此时的\(L(x, \alpha, \beta)\) 就只是和\(x\)有关的函数，定义这个函数为 \[\theta_{P}(x)=\max\limits_{\alpha, \beta:\alpha_{i}\geq 0}L(x, \alpha, \beta) \] 下面通过考虑\(x\)是否满足约束条件来分析\(\theta_{P}\)这个函数。 如果某些\(x\)不满足约束条件，即\(c_{i}(x)>0\)或\(h_{j}(x)\neq 0\), 则反过来 再考虑求\(\theta_{P}(x)\)最大值时的\(\alpha_{i}, \beta_{j}\) , 可以看出此时 不存在了，因为只要\(c_{i}(x)>0\)或\(h_{j}(x)\neq 0\)，L就不会存在一个确定的 \(\alpha_{i}, \beta_{j}\)使得L取最大值。也就是\(\theta_{P}(x)\)最大值是 \(+\infty\); 如果有\(x\)满足约束条件，则\(\theta_{P}(x)\)取最大值时 \(\sum_{j=1}^{l}\beta_{j}h_{j}(x)=0\) , 且 \(\sum_{i=1}^{k}\alpha_{i}c_{i}(x)=0\), 这样就有 \[\theta_{P}(x)=\max\limits_{\alpha, \beta:\alpha_{i}\geq 0}L(x, \alpha, \beta)=f(x)\] f(x)可以视为一个常量，常量的最大值就是本身。则在满足约束条件下 \[\min\limits_{x}\theta_{P}(x)=\min\limits_{x}\max\limits_{\alpha, \beta:\alpha_{i}\geq 0}L(x, \alpha, \beta)=\min\limits_{x}f(x)\] 即\(\min\limits_{x}\theta_{P}(x)\)与原始优化问题等价，所以常用此代表原始问 题，定义原始问题的最优值是：\[p^{'}=\min\limits_{x}\theta_{P}(x)\]

1.2.4.3 对偶问题

定义关于\(\alpha, \beta\)的函数： \[\theta_{D}(\alpha, \beta)=\min\limits_{x}L(x, \alpha, \beta)\] 此时等式右边是关于x的函数的最小化，x确定后，最小值就只跟\(\alpha, \beta\)有 关，所以是关于\(\alpha, \beta\)的函数。 考虑极大化\(\theta_{D}(\alpha, \beta)\), 即 \[\max\limits_{\alpha, \beta:\alpha_{i}\geq 0}\theta_{D}(\alpha,\beta)=\max\limits_{\alpha, \beta:\alpha_{i}\geq 0}\min\limits_{x}L(x, \alpha, \beta)\] 这就是原始问题的对偶问题。定义对偶问题的最优值：\[d^{'}=\max\limits_{\alpha, \beta:\alpha_{i}\geq 0}\theta_{D}(\alpha, \beta)\]

1.2.4.4 原始问题和对偶问题关系

定理：若原始问题和对偶问题都有最优值，则\[d^{'}\leq p^{'}\] 证明：对任意的\(\alpha, \beta, x\)有 \[ \theta_{D}(\alpha, \beta)=\min\limits_{x}L(x, \alpha, \beta)\leq L(x, \alpha, \beta) \leq \max\limits_{\alpha, \beta:\alpha_{i}\geq 0}L(x, \alpha, \beta)=\theta_{P}(x) \] 由于原始问题和对偶问题都有最优值，则 \[\max\limits_{\alpha, \beta:\alpha_{i}\geq 0}\theta_{D}(\alpha, \beta)\leq \min\limits_{x}\theta_{P}(x)\] 即 \[d^{'}=\max\limits_{\alpha, \beta:\alpha_{i}\geq 0}\min\limits_{x}L(x, \alpha, \beta) \leq \min\limits_{x}\max\limits_{\alpha, \beta:\alpha_{i}\geq 0}L(x, \alpha, \beta)=p^{'}\] 也就是说原始问题的最优值不小于对偶问题的最优值，但是要通过对偶问题求解原始 问题，就必须使得原始问题的最优值与对偶问题的最优值相等，于是可以得出下面的 推论：
设\(x^{'}\) 和\(\alpha^{'}, \beta^{'}\)分别是原始问题和对偶问题的解，若 \(d^{'}=p^{'}\)，那么\(x^{'}\) 和\(\alpha^{'}分别是原始问题和对偶问题的最优 解。所以当原始问题和对偶问题的最优值相等时，可以用求对偶问题来求原始问题， 前提是对偶问题求解更容易。但是要使\(d^{'}=p^{'}\)，则必须满足KKT条件。

1.2.4.5 KKT条件

定理：对于原始问题和对偶问题，假设函数f(x)和ci(x)是凸函数，hi(x)是仿 射函数（由多项式构成的函数如h(x)=Ax+b, A是矩阵，x，b是向量）, 并且假设不等 式约束ci(x)是严格可行的，即存在x，对所有i有ci(x)<0, 则存在x'和 α', β'使得x'是原始问题的最优解，α', β'是对 偶问题的最优解，且 \[d^{'}=p^{'}=L(x^{'}, \alpha^{'}, \beta^{'})\] 定理：按照上面的定理，x'是原始问题的最优解，α', β'是对偶 问题的最优解的充要条件是x'和α', β'满足下面的KKT条件 $$

\begin{cases} 1, \bigtriangledown_{x}L(x^{'}, \alpha^{'}, \beta^{'} &= 0\\ 2, \bigtriangledown_{\alpha}L(x^{'}, \alpha^{'}, \beta^{'} &= 0\\ 3, \bigtriangledown_{\beta}L(x^{'}, \alpha^{'}, \beta^{'} &= 0\\ 4, \alpha_{i}^{'}c_{i}(x^{'}) &= 0, i=1, 2, ..., k\\ 5, c_{i}(x^{'}) &\leq 0, i=1, 2, ..., k\\ 6, \alpha_{i}^{'} &\geq 0, i=1, 2, ..., k\\ 7, h_{j}(x^{'}) &=0, j=1, 2, ..., l\\ \end{cases}

$$ 前面3个条件是解析函数的知识，对各个变量的偏导数为0，后面4个条件就是原始问题 的约束条件以及拉格朗日乘子需要满足的约束条件。

1.3 cordic算法

1.3.1 背景

三角函数的计算是个复杂的主题，有计算机之前，人们通常通过查找三角函数表来计 算任意角度的三角函数的值。这种表格在人们刚刚产生三角函数的概念的时候就已经 有了，它们通常是通过从已知值（比如sin(π/2)=1）开始并重复应用半角和和差公式 而生成。现在有了计算机，三角函数表便推出了历史的舞台。但是像我这样的喜欢刨 根问底的人，不禁要问计算机又是如何计算三角函数值的呢。最容易想到的办法就是 利用级数展开，比如泰勒级数来逼近三角函数，只要项数取得足够多就能以任意的精 度来逼近函数值。除了泰勒级数逼近之外，还有其他许多的逼近方法，比如切比雪夫 逼近、最佳一致逼近和Padé逼近等。所有这些逼近方法本质上都是用多项式函数来近 似我们要计算的三角函数，计算过程中必然要涉及到大量的浮点运算。在缺乏硬件乘 法器的简单设备上（比如没有浮点运算单元的单片机），用这些方法来计算三角函数 会非常的费时。为了解决这个问题，J. Volder于1959年提出了一种快速算法，称之为 cordic(coordinate rotation digital computer) 算法，这个算法只利用移位和加减 运算，就能计算常用三角函数值，如sin，cos，sinh，cosh等函数。 J. Walther在 1974年在这种算法的基础上进一步改进，使其可以计算出多种超越函数，更大的扩展 了cordic 算法的应用。因为cordic 算法只用了移位和加法，很容易用纯硬件来实现， 因此我们常能在fpga运算平台上见到它的身影。不过，大多数的软件程序员们都没有 听说过这种算法，也更不会主动的去用这种算法。其实，在嵌入式软件开发，尤其是 在没有浮点运算指令的嵌入式平台（比如定点型dsp）上做开发时，还是会遇上可以用 到cordic 算法的情况的，所以掌握基本的cordic算法还是有用的。

1.3.2 从二分查找法说起

先从一个例子说起，知道平面上一点在直角坐标系下的坐标（X,Y）=（100，200）， 如何求的在极坐标系下的坐标（ρ,θ）。用计算器计算一下可知答案是（223.61， 63.435），见图\ref{img-cordic1}所示。

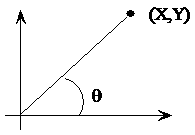cordic1.jpg 为了突出重点，这里我们只讨论X和Y都为正数的情况。这时\(θ=atan(y/x)\)。求θ 的过程也就是求atan 函数的过程。cordic算法采用的想法很直接，将（X，Y）旋转一 定的度数，如果旋转完纵坐标变为了0，那么旋转的度数就是θ。坐标旋转的公式可能 大家都忘了，这里把公式列出了。设（x,y）是原始坐标点，将其以原点为中心，顺时 针旋转θ之后的坐标记为（x’,y’）,则有如下公式： $$ f(x)=\left\{

\begin{aligned} x' & = & x\cos(\Theta) + ysin(\Theta) \\ y' & = & -x\sin(\Theta) + ycos(\Theta) \\ \end{aligned}

\right. \[ 也可以写成矩阵形式： \] {x' \choose y'}={cos(Θ) \quad sin(Θ) \choose -sin(Θ) \quad cos(Θ)}{x \choose y} \[ 如何旋转呢，可以借鉴二分查找法的思想。我们知道θ的范围是0到90度。那么就先旋 转45度试试。 \] {212.13 \choose 70.711} = {cos(45ˆ) \quad sin(45ˆ) \choose -sin(45ˆ) \quad cos(45ˆ)}{100 \choose 200}\[ 旋转之后纵坐标为70.71，还是大于0，说明旋转的度数不够，接着再旋转22.5度（45 度的一半）。 \]{223.04 \choose -15.85} = {cos(45ˆ/2) \quad sin(45ˆ/2) \choose -sin(45ˆ/2) \quad cos(45ˆ/2)} {212.13 \choose 70.711} \[ 这时总共旋转了45+22.5=67.5度。结果纵坐标变为了负数，说明θ<67.5度，这时就要 往回转，还是二分查找法的思想，这次转11.25度。 \]{221.85 \choose 27.967} = {cos(-45ˆ/4) \quad sin(-45ˆ/4) \choose -sin(-45ˆ/4) \quad cos(-45ˆ/4)} {223.04 \choose -15.851} \[ 这时总共旋转了45+22.5-11.25=56.25度。又转过头了，接着旋转，这次顺时针转 5.625度。 \]{223.52 \choose 6.0874} = {cos(45ˆ/8) \quad sin(45ˆ/8) \choose -sin(45ˆ/8) \quad cos(45ˆ/8)} {221.85 \choose 27.967} $$ 这时总共旋转了45+22.5-11.25+5.625=61.875度。这时纵坐标已经很接近0了。我们只 是说明算法的思想，因此就不接着往下计算了。计算到这里我们给的答案是 61.875±5.625。二分查找法本质上查找的是一个区间，因此我们给出的是θ值的一个 范围。同时，坐标到原点的距离ρ也求出来了，ρ=223.52。与标准答案比较一下计算 的结果还是可以的。旋转的过程图示如\ref{img-trans}。

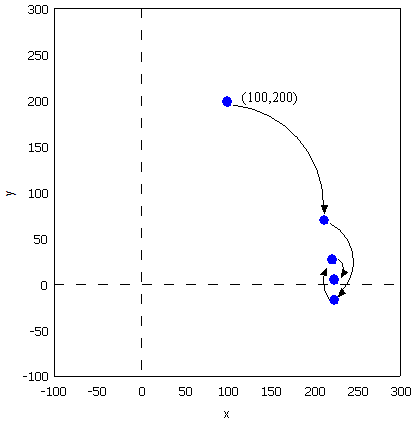cordic2.jpg 可能有读者会问，计算中用到了sin函数和cos函数，这些值又是怎么计算呢。很简单， 我们只用到很少的几个特殊点的sin 函数和cos 函数的值，提前计算好存起来，用时 查表。 

#include <stdio.h>
#include <stdlib.h>
        double my_atan2(double x, double y);
        int main(void)
        {
            double z = my_atan2(100.0, 200.0);
            printf("\n z = %f \n", z);

            return 0;
        }

        double my_atan2(double x, double y)
        {
            const double sine[] =
        {0.7071067811865,0.3826834323651,0.1950903220161,0.09801714032956, 
        0.04906767432742,0.02454122852291,0.01227153828572,0.006135884649154,0.003067956762966 
        ,0.001533980186285,7.669903187427045e-4,3.834951875713956e-4,1.917475973107033e-4, 
        9.587379909597735e-5,4.793689960306688e-5,2.396844980841822e-5 
        };

            const double cosine[] =
        {0.7071067811865,0.9238795325113,0.9807852804032,0.9951847266722, 
        0.9987954562052,0.9996988186962,0.9999247018391,0.9999811752826,0.9999952938096, 
        0.9999988234517,0.9999997058629,0.9999999264657,0.9999999816164,0.9999999954041,
        0.999999998851,0.9999999997128
        };

    int i = 0;
    double x_new, y_new;
    double angleSum = 0.0;
    double angle = 45.0;

    for(i = 0; i < 15; i++)
    {
    if(y > 0)
    {
        x_new = x * cosine[i] + y * sine[i];
        y_new = y * cosine[i] - x * sine[i];
        x = x_new;
        y = y_new;
        angleSum += angle;
    }
    else
    {
        x_new = x * cosine[i] - y * sine[i];
        y_new = y * cosine[i] + x * sine[i];
        x = x_new;
        y = y_new;
        angleSum -= angle;
    }
    printf("Debug: i = %d angleSum = %f, angle = %f\n", i, angleSum, angle);
    angle /= 2;
    }
    return angleSum;
}

程序运行的输出结果如下： 

Debug: i = 0 angleSum = 45.000000, angle = 45.000000
Debug: i = 1 angleSum = 67.500000, angle = 22.500000
Debug: i = 2 angleSum = 56.250000, angle = 11.250000
Debug: i = 3 angleSum = 61.875000, angle = 5.625000
Debug: i = 4 angleSum = 64.687500, angle = 2.812500
Debug: i = 5 angleSum = 63.281250, angle = 1.406250
Debug: i = 6 angleSum = 63.984375, angle = 0.703125
Debug: i = 7 angleSum = 63.632813, angle = 0.351563
Debug: i = 8 angleSum = 63.457031, angle = 0.175781
Debug: i = 9 angleSum = 63.369141, angle = 0.087891
Debug: i = 10 angleSum = 63.413086, angle = 0.043945
Debug: i = 11 angleSum = 63.435059, angle = 0.021973
Debug: i = 12 angleSum = 63.424072, angle = 0.010986
Debug: i = 13 angleSum = 63.429565, angle = 0.005493
Debug: i = 14 angleSum = 63.432312, angle = 0.002747
z = 63.432312

1.3.3 减少乘法运算

现在已经有点cordic算法的样子了，但是我们看到没次循环都要计算4次浮点数的乘法 运算，运算量还是太大了。还需要进一步的改进。改进的切入点当然还是坐标变换的 过程。我们将坐标变换公式变一下形。 \[{x' \choose y'} = {cos(\Theta) \quad sin(\Theta) \choose -sin(\Theta) \quad cos(\Theta)} {x \choose y} = cos(\Theta){1 \quad tan(\Theta) \choose -tan(\Theta) \quad 1}{x \choose y}\] 可以看出 cos(θ)可以从矩阵运算中提出来。我们可以做的再彻底些，直接把 cos(θ) 给省略掉。省略cos(θ)后发生了什么呢，每次旋转后的新坐标点到原点的距 离都变长了，放缩的系数是1/cos(θ)。不过没有关系，我们求的是θ，不关心ρ的改 变。这样的变形非常的简单，但是每次循环的运算量一下就从4次乘法降到了2次乘法 了。还是给出 C 语言的实现： 

double my_atan3(double x, double y)
{
    const double tangent[] =
{1.0,0.4142135623731,0.1989123673797,0.09849140335716,0.04912684976947, 
0.02454862210893,0.01227246237957,0.006136000157623,0.003067971201423,
0.001533981991089,7.669905443430926e-4,3.83495215771441e-4,1.917476008357089e-4,
9.587379953660303e-5,4.79368996581451e-5,2.3968449815303e-5
             };


    int i = 0;
    double x_new, y_new;
    double angleSum = 0.0;
    double angle = 45.0;

    for(i = 0; i < 15; i++)
    {
    if(y > 0)
    {
        x_new = x + y * tangent[i];
        y_new = y - x * tangent[i];
        x = x_new;
        y = y_new;
        angleSum += angle;
    }
    else
    {
        x_new = x - y * tangent[i];
        y_new = y + x * tangent[i];
        x = x_new;
        y = y_new;
        angleSum -= angle;
    }
    printf("Debug: i = %d angleSum = %f, angle = %f, ρ = %f\n", i, angleSum, angle, hypot(x,y));
    angle /= 2;
    }
    return angleSum;
}

计算的结果是： 

Debug: i = 0 angleSum = 45.000000, angle = 45.000000, ρ = 316.227766
Debug: i = 1 angleSum = 67.500000, angle = 22.500000, ρ = 342.282467
Debug: i = 2 angleSum = 56.250000, angle = 11.250000, ρ = 348.988177
Debug: i = 3 angleSum = 61.875000, angle = 5.625000, ρ = 350.676782
Debug: i = 4 angleSum = 64.687500, angle = 2.812500, ρ = 351.099697
Debug: i = 5 angleSum = 63.281250, angle = 1.406250, ρ = 351.205473
Debug: i = 6 angleSum = 63.984375, angle = 0.703125, ρ = 351.231921
Debug: i = 7 angleSum = 63.632813, angle = 0.351563, ρ = 351.238533
Debug: i = 8 angleSum = 63.457031, angle = 0.175781, ρ = 351.240186
Debug: i = 9 angleSum = 63.369141, angle = 0.087891, ρ = 351.240599
Debug: i = 10 angleSum = 63.413086, angle = 0.043945, ρ = 351.240702
Debug: i = 11 angleSum = 63.435059, angle = 0.021973, ρ = 351.240728
Debug: i = 12 angleSum = 63.424072, angle = 0.010986, ρ = 351.240734
Debug: i = 13 angleSum = 63.429565, angle = 0.005493, ρ = 351.240736
Debug: i = 14 angleSum = 63.432312, angle = 0.002747, ρ = 351.240736
z = 63.432312

1.3.4 消除乘法运算

我们已经成功的将乘法的次数减少了一半，还有没有可能进一步降低运算量呢？还要 从计算式入手。第一次循环时，tan(45)=1，所以第一次循环实际上是不需要乘法运算 的。第二次运算呢？tan(22.5)=0.4142135623731,很不幸，第二次循环乘数是个很不 整的小数。是否能对其改造一下呢？答案是肯定的。第二次选择22.5度是因为二分查 找法的查找效率最高。如果选用个在22.5到45度之间的值，查找的效率会降低一些。 如果稍微降低一点查找的效率能让我们有效的减少乘法的次数，使最终的计算速度提 高了，那么这种改进就是值得的。我们发现tan(26.565051177078)=0.5，如果我们第 二次旋转采用26.565051177078度，那么乘数变为0.5，如果我们采用定点数运算的话 （没有浮点协处理器时为了加速计算我们会大量的采用定点数算法）乘以0.5就相当于 将乘数右移一位。右移运算是很快的，这样第二次循环中的乘法运算也被消除了。类 似的方法，第三次循环中不用11.25度，而采用 14.0362434679265 度。 tan(14.0362434679265)= 1/4 乘数右移两位就可以了。剩下的都以此类推。 

tan(45)= 1
tan(26.565051177078)= 1/2
tan(14.0362434679265)= 1/4
tan(7.1250163489018)= 1/8
tan(3.57633437499735)= 1/16
tan(1.78991060824607)= 1/32
tan(0.8951737102111)= 1/64
tan(0.4476141708606)= 1/128
tan(0.2238105003685)= 1/256

还是给出C语言的实现代码，我们采用循序渐进的方法，先给出浮点数的实现（因为用 到了浮点数，所以并没有减少乘法运算量，查找的效率也比二分查找法要低，理论上 说这个算法实现很低效。不过这个代码的目的在于给出算法实现的示意性说明，还是 有意义的）。 

double my_atan4(double x, double y)
{
    const double tangent[] = {1.0, 1/2.0, 1/4.0, 1/8.0, 1/16.0,
                  1/32.0, 1/64.0, 1/128.0, 1/256.0, 1/512.0,
                  1/1024.0, 1/2048.0, 1/4096.0, 1/8192.0, 1/16384.0
                 };
    const double angle[] = {45.0, 26.565051177078, 14.0362434679265,
7.1250163489018, 3.57633437499735, 
                1.78991060824607, 0.8951737102111,
0.4476141708606, 0.2238105003685, 0.1119056770662, 
                0.0559528918938, 0.027976452617,
0.01398822714227, 0.006994113675353, 0.003497056850704 
               };

    int i = 0;
    double x_new, y_new;
    double angleSum = 0.0;

    for(i = 0; i < 15; i++)
    {
    if(y > 0)
    {
        x_new = x + y * tangent[i];
        y_new = y - x * tangent[i];
        x = x_new;
        y = y_new;
        angleSum += angle[i];
    }
    else
    {
        x_new = x - y * tangent[i];
        y_new = y + x * tangent[i];
        x = x_new;
        y = y_new;
        angleSum -= angle[i];
    }
    printf("Debug: i = %d angleSum = %f, angle = %f, ρ = %f\n", i, angleSum, angle[i], hypot(x, y));
    }
    return angleSum;
}

程序运行的输出结果如下： 

Debug: i = 0 angleSum = 45.000000, angle = 45.000000, ρ = 316.227766
Debug: i = 1 angleSum = 71.565051, angle = 26.565051, ρ = 353.553391
Debug: i = 2 angleSum = 57.528808, angle = 14.036243, ρ = 364.434493
Debug: i = 3 angleSum = 64.653824, angle = 7.125016, ρ = 367.270602
Debug: i = 4 angleSum = 61.077490, angle = 3.576334, ρ = 367.987229
Debug: i = 5 angleSum = 62.867400, angle = 1.789911, ρ = 368.166866
Debug: i = 6 angleSum = 63.762574, angle = 0.895174, ρ = 368.211805
Debug: i = 7 angleSum = 63.314960, angle = 0.447614, ρ = 368.223042
Debug: i = 8 angleSum = 63.538770, angle = 0.223811, ρ = 368.225852
Debug: i = 9 angleSum = 63.426865, angle = 0.111906, ρ = 368.226554
Debug: i = 10 angleSum = 63.482818, angle = 0.055953, ρ = 368.226729
Debug: i = 11 angleSum = 63.454841, angle = 0.027976, ρ = 368.226773
Debug: i = 12 angleSum = 63.440853, angle = 0.013988, ρ = 368.226784
Debug: i = 13 angleSum = 63.433859, angle = 0.006994, ρ = 368.226787
Debug: i = 14 angleSum = 63.437356, angle = 0.003497, ρ = 368.226788
z = 63.437356

有了上面的准备，我们可以来讨论定点数算法了。所谓定点数运算，其实就是整数运算。我们用256 表示1度。这样的话我们就可以精确 到1/256=0.00390625 度了，这对于大多数的情况都是足够精确的了。256 表示1度，那么45度就是 45*256 = 115200。其他的度数以此类 推, 迭代次数见表\ref(tbl-dedaicishu)。

Table 1: 迭代次数
number angle anglex256 integer
1 45.0 11520 11520
2 26.565051177078 6800.65310133196 6801
3 14.0362434679265 3593.27832778918 3593
4 7.1250163489018 1824.00418531886 1824
5 3.57633437499735 915.541599999322 916
6 1.78991060824607 458.217115710994 458
7 0.8951737102111 229.164469814035 229
8 0.4476141708606 114.589227740302 115
9 0.2238105003685 57.2954880943458 57
10 0.1119056770662 28.647853328949 29
11 0.0559528918938 14.3239403248137 14
12 0.027976452617 7.16197186995294 7
13 0.01398822714227 3.58098614841984 4
14 0.006994113675353 1.79049310089035 2
15 0.003497056850704 0.8952465537802 1

C 代码如下： 

int my_atan5(int x, int y)
{
    const int angle[] = {11520, 6801, 3593, 1824, 916, 458, 229, 115, 57,
29, 14, 7, 4, 2, 1}; 

    int i = 0;
    int x_new, y_new;
    int angleSum = 0;

    x *= 1024;// 将 X Y 放大一些，结果会更准确
    y *= 1024;

    for(i = 0; i < 15; i++)
    {
    if(y > 0)
    {
        x_new = x + (y >> i);
        y_new = y - (x >> i);
        x = x_new;
        y = y_new;
        angleSum += angle[i];
    }
    else
    {
        x_new = x - (y >> i);
        y_new = y + (x >> i);
        x = x_new;
        y = y_new;
        angleSum -= angle[i];
    }
    printf("Debug: i = %d angleSum = %d, angle = %d\n", i, angleSum, angle[i]);
    }
    return angleSum;
}

计算结果如下: 

Debug: i = 0 angleSum = 11520, angle = 11520
Debug: i = 1 angleSum = 18321, angle = 6801
Debug: i = 2 angleSum = 14728, angle = 3593
Debug: i = 3 angleSum = 16552, angle = 1824
Debug: i = 4 angleSum = 15636, angle = 916
Debug: i = 5 angleSum = 16094, angle = 458
Debug: i = 6 angleSum = 16323, angle = 229
Debug: i = 7 angleSum = 16208, angle = 115
Debug: i = 8 angleSum = 16265, angle = 57
Debug: i = 9 angleSum = 16236, angle = 29
Debug: i = 10 angleSum = 16250, angle = 14
Debug: i = 11 angleSum = 16243, angle = 7
Debug: i = 12 angleSum = 16239, angle = 4
Debug: i = 13 angleSum = 16237, angle = 2
Debug: i = 14 angleSum = 16238, angle = 1
z = 16238

16238/256=63.4296875度，精确的结果是63.4349499度，两个结果的差为0.00526，还 是很精确的。到这里cordic算法的最核心的思想就介绍完了。当然，这里介绍的只是 cordic算法最基本的内容，实际上，利用cordic 算法不光可以计算 atan 函数，其他 的像 sin，cos，sinh，cosh 等一系列的函数都可以计算，不过那些都不在本文的讨 论范围内了。另外，每次旋转时到原点的距离都会发生变化，而这个变化是确定的， 因此可以在循环运算结束后以此补偿回来，这样的话我们就同时将（ρ,θ）都计算出 来了。

2 滤波算法

2.1 中值滤波

中值滤波法是一种非线性的信号处理技术。中值滤波将一个长度为给定奇数的移动窗 作用于序列，该窗中心位置的值用窗口内各点排序后的中值替代，待处理点的前面后 面数据数目一样。中值滤波器能有效的克服因为偶然因素引起的波动干扰，比如脉冲 噪声。因为在窗口内排序后，最小的和最大的值将排在窗口两边，滤波后的序列将不 会包含这些点。所以滤除脉冲比较有效。

2.2 全期平滑滤波

简单的全期平滑法是对时间数列的过去数据一个不漏的全部加以同等利用；

2.3 移动平滑滤波

移动平滑法不考虑较远期的数据，并在加权移动平均法中给予近期资料更大的权重； 通常做法是，使用一个队列或数组作为移动窗口，有新数据时就插入队列头，当队列 数据满了，则再增加一个数据就从队尾去除一个数据；每有新数据时就用队列数据的 平均值作为输出替代。

  • 优点：能够比较好的抑制随机噪声，如果窗口选择大，则最终输出数据平滑效果好；
  • 缺点：对新数据的权重比较低，导致对新输入不够敏感，比较迟滞。

2.4 指数平滑滤波

指数平滑法则兼容了全期平均和移动平均所长，不舍弃过去的数据，但是仅给与逐渐 减弱的影响权重，即随着数据的远离，赋予逐渐收敛于零的权重。

2.4.1 指数平滑的公式

\begin{equation} \label{equ-pinghua} s_{t} = \alpha{}.y_{t} + (1-\alpha{}).s_{t-1} \end{equation}
  1. st: 当前时刻t的平滑输出值；
  2. yt: 当前时刻t的实际输入值；
  3. st-1: 上一时刻t-1的平滑值；
  4. α: 平滑比例常数，取值范围[0, 1]

由式子\ref{equ-pinghua}可知：

  1. st是yt和st-1的加权算术平均数，随着\alpha取值的大小变化，决定 yt和st-1对st的影响程度，当\alpha取1时，\(s_{t}=y_{t}\); 当取0 时，\(s_{t}=s_{t-1}\).
  2. st具有逐期追溯性质，可探源至st-(t-t)为止。包括全部数据，其过程中， 平滑常数以指数形式递减，所以称为指数平滑法。如果能够找到y1以前的历 史数据，那么初始值s1的确定是可行的，数据较少时可以用全期平均，移动 平均法；数据较多时，可以用最小二乘法。但不能使用指数平滑法本身确定初始 值，因为数据会匮竭。如果仅有从y1开始的数据，那么确定初始值的方法有：
    1. 取s1等于y1；
    2. 待积累若干数据后，取s1等于前面若干数据的简单算术平均数，如： \(s_{1}=（y_{1}+ y_{2}+y_{3}）/3\)等等。

2.4.2 一次指数平滑

设时间序列为\(y_{1}, y_{2}, ..., y_{t}...\)，则一次指数平滑 公式如式\ref{equ-pinghua}.通过展开可以有

\begin{equation} \label{equ-pinghuazk} s_{t} = \alpha.\sum_{j=0}^{t-1}(1-\alpha)^{j}y_{t-j}+(1-\alpha)^{t}s_{0} \end{equation}

由于\(0<\alpha<1\), 当\(t\Rightarrow \infty\)时， \((1-\alpha)^{t}\Rightarrow 0\)，式子\ref{equ-pinghuazk}变为

\begin{equation} s_{t} = \alpha\sum_{j=0}^{\infty}(1-\alpha)^{j}y_{t-j} \end{equation}

由此可见，st实际上是\(y_{t}, y_{t-1}...\)的加权平均，加权系数分别为 \(\alpha, \alpha(1-\alpha), \alpha(1-\alpha)^{2}...\)是按照几何级数递减。 越近的数据，权重越大，越远的数据，权重越小，且权重之和等于1

\begin{equation} \alpha\sum_{j=0}^{\infty}(1-\alpha)^{j} = 1 \end{equation}

因为加权系数符合指数规律，且又具有平滑数据的功能，所以称为指数平滑。

2.4.3 二次指数平滑

当时间序列没有明显的趋势变动时，使用第t周期一次指数平滑就能直接预测第t+1 期之值。但当时间序列的变动出现直线趋势时，用一次指数平滑法来预测仍存在着 明显的滞后偏差。因此，也需要进行修正。 修正的方法也是在一次指数平滑 的基础上再作二次指数平滑，利用滞后偏差的规律找出曲线的发展方向和发展趋势， 然后建立直线趋势预测模型。故称为二次指数平滑法。 设一次指数平滑为\(s_{t}\)，则二次指数平滑\(s_{t}^{(2)}\)的计算公式为

\begin{equation} s_{t}^{(2)} = \alpha{}s_{t}^{(1)}+(1-\alpha)s_{t-1}^{(2)} \end{equation}

若yt从某时刻开始具有直线趋势，且认为未来时期亦按此直线趋势变化，则可以 用二次指数平滑。

2.4.4 三次指数平滑

若时间序列的变动呈现出二次曲线趋势，则需要用三次指数平滑法。三次指数平滑 是在二次指数平滑的基础上再进行一次平滑，其计算公式为

\begin{equation} s_{t}^{(3)}=\alpha{}s_{t}^{(2)}+(1-\alpha)s_{t-1}^{(3)} \end{equation}
  • 指数平滑系数：指数平滑法的计算中，关键是 的取值大小，但 的取值又容易受主 观影响，因此合理确定 的取值方法十分重要，一般来说，如果数据波动较大， 值 应取大一些，可以增加近期数据对预测结果的影响。如果数据波动平稳， 值应取小 一些。经验判断法：
    1. 当时间序列呈现较稳定的水平趋势时，应选较小的 值，一般可在0.05～0.20之间取值；
    2. 当时间序列有波动，但长期趋势变化不大时，可选稍大的 值，常在0.1～0.4之间取值；
    3. 当时间序列波动很大，长期趋势变化幅度较大，呈现明显且迅速的上升或下降趋 势时，宜选择较大的 值，如可在0.6～0.8间选值，以使预测模型灵敏度高些，能迅速跟上数据的变化；
    4. 当时间序列数据是上升（或下降）的发展趋势类型， 应取较大值，在0.6~1之间。

3 图像处理

数字图像定义：数字图像指的是一个被采样和量化后的二维函数(该二维函数由光学方 法产生), 采用等距离矩形网格采样，对幅度进行等间隔量化。至此一副数字图像是一 个被量化的采样数值的二维矩阵，对维度、量化进行推广，还可以得到广义图像定义。

3.1 概念

  • 数字化：是将一幅图像从其原来的形式转换为数字形式的处理过程。数字化的逆过 程是显示；
  • 扫描：指对一副图像内给定位置的寻址，在扫描过程中被寻址的最小单元是像素；
  • 采样：是指在一副图像的每个像素位置上测量灰度值。采样通常由一个图像传感器 来完成，将每个像素处的亮度转换成与其成正比的电压值；
  • 量化：是将测量的灰度值用一个整数表示，离散化；
  • 对比度：是指一幅图像中灰度反差的大小；
  • 灰度分辨率：是指值的单位幅度上包含的灰度级数，如用8bit存储一副数字图像， 其灰度级为256；
  • 采样密度：是指在图像上单位长度包含的采样点数(pixel/mm)；
  • 像素间距：是指像素点之间的距离长度，采样密度的倒数(mm/pixel)；
  • 放大率：指图像中物体与其对应的景物中物体的大小比例关系；

3.2 其他

  • 人眼只能分辨约40级灰度，也就是如果黑白之间的灰度范围被分为40个以上的等分， 相邻的灰度级可能对人眼对来说看起来是相同的；

4 机器学习

4.1 基本概念

  • 过拟合：overfitting，一个过分复杂的系统单纯对训练样本集能获得完美的表现， 但是对于新鲜样本则可能不令人满意的现象称为过拟合；
  • 样本集合：一般样本集合可以分为
    1. training set：训练集，用于训练得出我们的候选算法集合；
    2. validation set：验证集，用于在候选算法集合中选出一个错误率最低的算法；
    3. test set：测试集，用于测试我们选出的这个错误率最低的算法；
  • 样本集打散：假如存在一个N个样本的样本集能够被一个函数集中的函数按照2N 种所有可能形式分为2类，则称该函数集能够把样本数为N的样本集打散(shatter)， 其实这里的2类只是一种特例的标记方式，可以延伸到任意一种标记方式，官方的定 义为：对于给定集合S={X1, …, Xi}, 如果一个假设类H能够实现集合S中所有元素 的任意一种标记方式，则称H能够打散S，这里的集合S就是上面的N个样本，假设类H 就是上面的函数集，任意一种标记方式的一种特列就是上面的分成2类，如果把 2N种分类的每一种看做一个学习问题，那么2N种学习问题就可以用N个点定义；
  • VC维：依照样本集打散的概念，该函数集的VC维就是用这个函数集中的函数能够打 散的最大样本集的样本数目, 而所谓的打散，指的是这个函数集能够按照任意个数 的类别来分开这么多个样本，也就是说，若存在N个样本的样本集能够被函数集打散， 而不存在N+1个样本集能够打散，则该函数集的VC维就是N。另外，若对于任意的样 本数，总能找到一个样本集能够被这个函数集打散，则函数集的VC维就是无穷大， 当我们在衡量一个函数集能否分类一堆样本时，理论上这个函数集的VC维越大则表 示这个函数集能够分类的样本数量越大，否则越小，但是在实际中，并不是说VC维 越大越有用，因为对样本进行分类时并不是说要做到0错误，只需要保证可接受的错 误率就行，这时对函数集的VC维要求就放宽了，一般函数集的VC维越大函数集越复 杂越难实现，所以实际中，常常用到的是VC维比较低的函数集；
  • PAC: Probably Approximately Correct，概率近似正确(学习模型) ，主要用于解 决这一的学习问题：由于我们采集的样本空间不能完全的满足真正的完整空间的数 据，所以我们的样本空间与现实的完整空间存在一定的误差，这将导致我们的学习 器通过对样本空间学习得来的经验不能完全的满足未来新数据的处理，所以提出了 PAC学习模型，以使得我们对满足未来新数据的错误率被限制在某常数\epsilon范围 内，\epsilon可以任意小；
  • inductive bias：归纳偏置，机器学习试图去建造一个可以学习的算法，用来预测 某个目标的结果。要达到此目的，要给于学习算法一些训练样本，样本说明输入与 输出之间的预期关系。然后假设学习器在预测中逼近正确的结果，其中包括在训练 中未出现的样本。既然未知状况可以是任意的结果，若没有其它额外的假设，这任 务就无法解决。这种关于目标函数的必要假设就称为归纳偏置；
  • generalization：一般化，指的是，我们通过样本集训练出的算法可以推广到未知 输入得到正确输出；
  • Loss function:损失函数，表示实际输出值与我们拟合算法输出值的差；

4.2 基本方法

4.2.1 最小二乘法

4.2.1.1 解法一

最小二乘法是为了求一组观察数据(变量X和Y)之间的函数关系Y=f(X)=ATX.其 中X是训练特征矩阵，Y是结果向量。应用条件如下

  1. 若变量间的函数形式根据理论分析或者以往的经验已经确定好了，只是其中某些参 数是未知的，则可以通过观察数据来确定这些参数；
  2. 若变量间的具体函数形式尚未确定，则需要通过观测数据来确定函数形式和参数；
  3. X必须是列满秩；

最终求得的A参数为\[A=(X^{T}X)^{-1}X^{T}Y\] 在选取的参数估计值A->a1', a2',…, ak', 应 使得变量Y的诸多观测值yi与其真值的估计值(又叫拟合值)，即f(Xi; a1, …, ak) 之差的平方和最小，用式子表示时，记残差vi为 \[ v_{i}=y_{i}-\hat{y_{i}}=y_{i}-f(X_{i}; a_{1}, ..., a_{k})\] 最小二乘法就是要求下面式子的最小值时的ai参数。 \[R=\sum_{i=1}^{n}v_{i}^{2}\] 在这个条件下，用数学中求极值的方法可以求出这些参数。根据数学分析中求函数极 值的条件

\begin{equation} \begin{cases} \frac{\partial R}{\partial a_{1}}=\frac{\partial\sum_{i=1}^{n}v_{i}^{2}}{\partial a_{1}}=0\\ \frac{\partial R}{\partial a_{2}}=\frac{\partial\sum_{i=1}^{n}v_{i}^{2}}{\partial a_{2}}=0\\ \frac{\partial R}{\partial a_{k}}=\frac{\partial\sum_{i=1}^{n}v_{i}^{2}}{\partial a_{k}}=0\\ \end{cases} \end{equation}

共得到k个方程，求这k个方程的联立解就可以求出ai'的值。

4.2.1.2 解法二

函数关系是\(Y=f(X)=A^{T}X\), 损失函数为平方差的和，写成矩阵的形式为 \[L(W)=(Y-XW)'(Y-XW)\] 可以看出L(W)是一个向量也算一个矩阵，则可以采用矩阵L对列向量W求导，并令其等 于0来计算出W的值。 \[\frac{dL}{dW}=-2X'Y+2X'XW=0\] 由此得 \[X'XW=X'Y\] 其中如果\(X'X\)的逆存在，最小二乘问题的解是： \[W=(X'X)^{-1}X'Y\]

4.2.2 核函数

核是一个函数K，对所有\(x, z \in{}X\)，满足： \[K(x, z) = <\phi{}(x).\phi{}(z)>\] 这里\(\phi\)是从X到特征空间F的映射。
核这个名字是从积分算子理论中来的，这个理论以核与其相关特征空间的关系的理论 为基础。对偶表达的一个重要结果是特征空间的维数不再影响计算。当不再显示表达 特征空间向量，而是通过计算核函数的值来计算内积时所需算子数目不一定与特征的 数目成比例。核的使用使得将数据隐式表达为特征空间，并在其中训练一个线性学习 器成为可能，从而越过了本来需要的计算特征映射的问题。关于训练样例的唯一信息 是他们在特征空间的Gram矩阵。这个句子又称为核矩阵。

4.3 k临近算法

K临近算法举例，已知若干电影(训练集)的标签有“爱情片”，“动作片”，而这些标 签大体是由这些电影中所含的打斗场景和接吻场景次数(特征)决定。现在有一部电影 已知打斗场景和接吻场景次数，但是标签未知，需要判断。则可以计算由这些特征组 成的样本点之间的距离，并选出离训练集中前k个最近的点，再统计这k个样本点的标 签占比，占比多的就是该新电影的标签。实例代码如下，我们有由createDataSet函数 生成一个测试样本和标签集，其中array的每个元素代表一个已知样本，而每个已知样 本的各个元素代表其特征值，labels给出了group的每个样本的标签；实质上也是欧式 距离的应用。 注意: 要运行必须要删除所有的中文注释。 

import numpy as np
import scipy as sp
import operator

def createDataSet():
    group = np.array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]])
    labels = ['A', 'A', 'B', 'B']
    return group, labels

# inX和dataSet的行向量应该是一致的
# 每个行代表一个样本
def classify0(inX, dataSet, labels, k):
    # dataSet是一个numpy array，shape属性包含行数和列数，比如shape[0]给出行数，shape[1]给出列数，这里我们需要行数，它对
    # 应于观察点(dataSet)的数目，列数对应每个点对应的特征项
    dataSetSize = dataSet.shape[0]
    # inX是一个list，这一行表示将inX复制总共dataSetSize次，tile函数第一个参数表示需要复制的量，第二个参数表示需要复制的
    # 形式，也就是说将inX复制dataSetSize行，1列，其维度满足dataSet
    matrExt = tile(inX, (dataSetSize, 1)) 
    # 开始计算inX和dataSet中每个样本的距离
    diffMat = matrExt - dataSet
    sqDiffMat = diffMat**2
    # 以列维度相加, 如果axis=0, 将以行维度进行相加，如果直接用sum()将会计算所有元素的和
    sqDistances = sqDiffMat.sum(axis=1) 
    distances = sqDistances**0.5
    # argsort函数返回数组值从小到大的索引值 
    sortedDistInddicies = distances.argsort() 
    # 建立一个空字典/哈希表/映射:键值为label;值为每个label出现的频率
    classCount={}
    # 这里主要进行投票
    for i in range(k):
        # 寻找到前K个距离最近点的标签，然后对每个标签在字典classCount里面统计出现的次数
        voteIlabel = labels[sortedDistInddicies[i]]
        # dict.get(key, default=None)
        # key 字典中要查找的键。default 如果指定键的值不存在，返回该默认值值。
        # 已labels为标签下标，统计每个标签所出现的频率
        classCount[voteIlabel]=classCount.get(voteIlabel, 0)+1
    # 最终得到的classCount大概长这样{'A': 3, 'C': 5, 'B': 2}，也就是意味着标签C出现的次数最多，目的就是要返回最多的，下
    # 面这行代码将字典排序成list，大的在前
    # classCount.items(), 将得到dict_items([('c', 5), ('b', 2), ('a', 3)])
    # operator.itemgetter(1)定义了一个函数，获取对象上的值，必须要作用到对象上才行
    # Python内置的排序函数sorted可以对list或者iterator进行排序;
    # 综合来看下面先将classCount转化为list，元素为元组，然后key指定排序时使用的排序方法(元组的第1个元素)，由reverse指定
    # 是逆序排序
    # 最后sortedClassCount形如[('c', 5), ('a', 3), ('b', 2)]
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse = True)
    # 返回'c'
    return sortedClassCount[0][0]

point0 = [0, 0]
g, l = createDataSet()
print("resualt: %r" %classify0(point0, g, l, 3))

4.4 决策树

4.4.0.1 信息熵

信息熵用来衡量信息量的大小

  • 若某个集合中不确定性越大，则信息量越大，熵越大；
  • 若某个集合中不确定性越小，则信息量越小，熵越小；

定义：一个值域为\({x_{1}...x_{n}}\)的随机变量X的信息熵H定义为： \[H(X) = E(I(X))\] 其中，E代表期望函数，I(X)是X的信息量，I(X)本身也是个随机变量，如果p是概率函 数，则H(X)可以表示为 \[H(X)=\sum_{i=1}^{n}p(x_{i})I(x_{i})=-\sum_{i=1}^{n}p(x_{i})log_{b}p(x_{i})\] 在这里b是对数所使用的底。

  • 当b=2时熵的单位是bit；
  • 当b=e时熵单位是nat；
  • 当b=10时熵单位是dit。
4.4.0.2 算法逻辑

构建决策树的过程，就是减小信息熵，减小不确定性。从而完整构造决策树模型。所 以我们需要在每一次选择分支属性时，计算这样分类所带来的信息熵的增益，增益越 大，不确定性越小，最终也就是我们要选择的分支属性。

  • 首先, 我们会在未进行任何分类前求取一个信息熵，这个信息熵涉及到只是简单的 求取样本标签的分布，然后按照公式求解信息熵。
  • 然后，在选用某一个属性作为分支属性后，我们需要计算每一个子分支中的样本标 签的分布，然后计算每个子样本的信息熵，最后加权平均（期望），求得总信息熵。
  • 计算前后两个信息熵的差值，选择最大的增益属性作为分支属性。一直递归下去， 对每一个子样本套用上述方法。直到所有的样本都被归类于某个叶节点，即不可再 分为止。

以上方法是 ID3 方法，还有更好的 C4.5 方法，C4.5方法选用信息增益比，克服 了ID3使用信息增益选择属性时偏向取值较多的属性的不足。

4.4.0.3 算法实例
  1. 计算香农熵

    根据信息熵的计算公式计算某个数据集中的信息熵。一组数据dataSet包含若干特征属 性和一个标签，即某个标签具有若干属性，每个标签和属性都有若干值。以某个标签 为基准计算所有标签值的香农熵。数据集可以用Excel表格表示，每一行代表一个数据， 每一列代表数据的一个特征，最后一列代表数据的标签，比如加速度值，每一行代表 采集的一次加速度值，包含3列xyz，表示3个轴的加速度分量，最后一列表示标签，可 以取'跑步','走路'等值，代码 

    # dataSet：数据集
def calcShannonEnt(dataSet):
    numEntries = len(dataSet)   
    labelCounts = {}            #标签，键是标签的值，值是每个标签值的个数
    for featVec in dataSet:     #featVec是dataSet中的某组数据记录
        currentLabel = featVec[-1] #featVec[-1]表示某组数据的标签
        # 统计每个标签值的个数
        if currentLabel not in labelCounts.keys(): 
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    # 计算每种标签值的频率以及香农熵统计
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2) #log base 2
    return shannonEnt
  2. 划分数据集

    指按照给定的特征以及特征的值提取出这样的数据集。代码 

    # dataSet：数据集
# axis：取值x或y或z
# value：表示某个x(yz)分量的值
# return：返回在dataSet中删除了axis列的样本，这些样本的axis列值等于value，
# 不等于value的样本属于另一个树分支
def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis] 
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet
  3. 选择最好的划分

    在不同的特征，不同的特征值情况下，计算被splitDataSet()提取出来的样本的香农 熵(按样本标签计算)。然后按照该特征下每个特征值占的比例计算该特征的香农熵总 和，再用原始熵减去这个熵得熵增益，得出按照该特征划分时的效果量化值。最后比 较每种按特征划分后的香农熵，找出最大香农熵的一种划分方式。 

    def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1      # 特征个数
    baseEntropy = calcShannonEnt(dataSet) #原始香农熵
    bestInfoGain = 0.0; bestFeature = -1
    # 遍历每个特征
    for i in range(numFeatures):        #iterate over all the features
        # python的list推导式
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)       #get a set of unique values
        newEntropy = 0.0
        # 遍历当前特征下每个特征值
        for value in uniqueVals:
            # 计算当前特征，当前特征值提取出的数据集
            subDataSet = splitDataSet(dataSet, i, value)
            # 计算当前特征值占该特征数量的比例
            prob = len(subDataSet)/float(len(dataSet))
            # 计算当前特征的加权香农熵
            newEntropy += prob * calcShannonEnt(subDataSet)     
        # 计算香农熵增益
        infoGain = baseEntropy - newEntropy
        # 提炼出最大香农熵增益下的特征序号
        if (infoGain > bestInfoGain):    
            bestInfoGain = infoGain      
            bestFeature = i
    return bestFeature                      #returns an integer
  4. 构造决策树

    采用递归将决策树存储在字典中，使用字典可以存在于字典中的特性。最终，字典将 是，使用特征标签作为key，其value要么是类别标签作为树的终止叶子节点，要么是 另一个字典，以此递归。 

    def createTree(dataSet, labels):  
    # 样本集的类别标签
    classList = [example[-1] for example in dataSet]  
    #类别标签完全相同则停止继续划分，返回类标签(叶子节点)  
    if classList.count(classList[0]) == len(classList):  
        return classList[0]  
    #遍历完所有的特征时返回出现次数最多  
    if len(dataSet[0]) == 1:  
        return majorityCnt(classList)       
    bestFeat = chooseBestFeatureToSplit(dataSet)  
    bestFeatLabel = labels[bestFeat]  
    # 每一级递归中用类别标签作为key，其value将是该标签的每个值
    myTree = {bestFeatLabel:{}}  
    # 删除一个特征
    del(labels[bestFeat])  
    # 得到的列表包含所有的属性值  
    featValues = [example[bestFeat] for example in dataSet]    
    uniqueVals = set(featValues)  
    # 遍历每个值作为字典的value
    for value in uniqueVals:  
        subLabels = labels[:]  
        # 其值就是上面的两个终止条件返回的类别标签
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)  
    return myTree

4.5 贝叶斯分类

贝叶斯分类一般是，训练集中有若干类样本ci, 每个样本有若干个特征构成特征向 量，这样不同的特征向量构成特征向量集合vj, 当我们获得新的特征向量v时，需 要判断其属于哪个类别。贝叶斯条件概率如下 \[p(c_{i}|v)=\frac{p(v|c_{i})p(c_{i})}{p(v)}\] 其中，p(ci|v)表示我们有了新的特征向量v，判断其属于某个类别c的概率，在计 算出所有类别后取其大者为v的类别。 p(v|ci)表示该类别c下特征v在训练集中的概率。 p(ci)表示该类别在训练集中的出现的概率。 p(v)表示该特征v在训练集中出现的概率。 往往我们在计算p(v|ci)时有困难，因为特征向量中每个特征之间可能还具有依赖 关系，而朴素贝叶斯思想就是假定特征向量中每个特征之间是相互独立的，则 p(v|ci)计算时可以计算所有子特征在类别c下的概率乘积。例如 某个医院早上收了六个门诊病人，如下表。

症状　 　职业　　 　疾病
　　打喷嚏　 护士　　　 感冒
　　打喷嚏　 农夫　　　 过敏
　　头痛　　 建筑工人　 脑震荡
　　头痛　　 建筑工人　 感冒
　　打喷嚏　 教师　　　 感冒
　　头痛　　 教师　　　 脑震荡

现在又来了第七个病人，是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大？ 根据贝叶斯定理得P(感冒|打喷嚏*建筑工人)=P(打喷嚏*建筑工人|感冒)*P(感冒)/P(打 喷嚏*建筑工人) , 假定"打喷嚏"和"建筑工人"这两个特征是独立的，因此，上面的等 式就变成了P(感冒|打喷嚏*建筑工人)=P(打喷嚏|感冒)*P(建筑工人|感冒)*P(感冒)/P(打 喷嚏)*P(建筑工人) 最终计算得P(感冒|打喷嚏*建筑工人)=0.66*0.33*0.5/0.5*0.33=0.66 因此，这个打喷嚏的建筑工人，有66%的概率是得了感冒。同理，可以计算这个病人患 上过敏或脑震荡的概率

4.6 支持向量机

4.7 回归分析

回归是一种极易理解的模型，就相当于\(y=f(x)\)，表明自变量x与因变量y的关系。最常见问题有如医生治病时的望、闻、问、切，之后 判定病人是否生病或生了什么病，其中的望闻问切就是获取自变量x，即特征数据，判断是否生病就相当于获取因变量y，即预测分类。 随机变量间的关系，可以从多个角度来分析, 并可以参考相关系数 。

  1. 从涉及的变量数量看
    • 简单相关：两个变量间；
    • 多重相关：多个变量间；
  2. 从变量相关关系的表现形式看：
    • 线性相关：散布图上样本接近一条直线；
    • 非线性相关：散布图上样本接近一条曲线；
  3. 从变量相关关系变化的方向看：
    • 正相关：变量同方向变化，同增同减；
    • 负相关：变量反方向变化，一增一减；
    • 不相关：无规律；

关于回归分析问题的一般步骤如下

  1. 寻找H函数：hypothesis，即模型假设；
  2. 构造J函数：即损失函数，比如最小二乘法；
  3. 求模型参数：想办法使得J函数最小求出模型参数，常用最大似然，梯度下降，这一套可以归咎为 最优化理论 。
4.7.0.1 线性回归

最简单的回归就是线性回归，包括单变量回归，和多变量回归。一个坐标系下(可以是n维)，有若干个点，找一直线(或其他图，圆)来最 大可能的近似这些点的走势趋势，然后使用最小二乘法等方法接触相应的参数，就是线性回归，另外线性回归 是以 高斯分布 为误差分 析模型。用向量来表示，数据集的模型可以这样表示 \[ h_{\theta}(x)=\theta^{T}\chi\] 也就是带了一系列的参数\(\theta\)和一系 列的维度变量\(x_{i}\), 这就是一个组合问题，已知一些数据，如何求里面的未知参数，给出一个最优解。 一个线性矩阵方程，直接求 解，很可能无法直接求解。有唯一解的数据集，微乎其微。基本上都是解不存在的超定方程组。因此，需要退一步，将参数求解问题，转 化为求最小误差问题，求出一个最接近的解，这就是一个松弛求解。 求一个最接近解，直观上，就能想到，误差最小的表达形式。仍然 是一个含未知参数的线性模型，一堆观测数据，其模型与数据误差最小的形式，模型与数据差的平方和最小, 这就是损失函数的来源。求 解方法有 \[ J(\theta)=\frac{\sum_{i=1}^{m}(h_{\theta}(x^{i})-y^{i})^{2}}{2}\]

  1. 最小二乘法：是一个直接的数学求解公式，不过它要求X是列满秩的；
  2. 梯度下降法：分别有梯度下降法，批梯度下降法，增量梯度下降。本质上，都是偏导数，步长/最佳学习率，更新，收敛的问题。这个 算法只是最优化原理中的一个普通的方法；
4.7.0.2 岭回归

如果在最小二乘法中\(X'X\)矩阵不是满秩，或者在其他情况下数值解不稳定，则可以 使用下面的解 \[W=(X'X+\lambda{}I_{n})^{-1}X'Y\] 上面的公式可以通过矩阵\(X'X\)上增加对角矩阵\(I_{n}\)的乘子\(\lambda \in R^{+}\)来得到，这里\(I_{n}\)是一个(n+1, n+1)项为0的单位矩阵，这就是岭回归。

4.7.0.3 逻辑回归

线性回归的鲁棒性很差，主要是由于线性回归在整个实数域内敏感度一样，而我们一般的数据点都是有一定范围。这时逻辑回归就用于限 制预测范围，比如常用的sigma函数将值域限制在[0, 1]范围。所以逻辑回归其实仅为在线性回归的基础上，套用一个逻辑函数，将线性 回归实数值域映射到一定小范围，另外逻辑回归 采用的是 伯努利分布 分析误差。 逻辑回归的模型 是一个非线性模型，sigmoid函数，又称逻辑回归函数。但是它本质上又是一个线性回归模型，因为除去sigmoid映射函 数关系，其他的步骤，算法都是线性回归的。可以说，逻辑回归，都是以线性回归为理论支持的。只不过，线性模型，无法做到sigmoid 的非线性形式，sigmoid可以轻松处理0/1分类问题。

4.8 神经网络

此处有斯坦福的课程网页：http://ufldl.stanford.edu/wiki/index.php/神经网络

  • 常用的激活函数
    1. 线性函数 \[ f(x)=k*x + c\]
    2. 斜面函数 \[ f(x) = \{ T, x>c k*x, |x|\leq{c} -T, x < -c \]

    3. 阈值函数 $$ f(x)=\{

      \begin{aligned} 1, x\geq c \\ 0, x < c \end{aligned}

      $$

4.8.1 概念

  • 超平面：n维超平面的表达方式为\(f(X)=W^{T}X+B\), 其中W和X都是n维向量，一般 W表示权重向量同时也是超平面的法向量，X表示特征向量，B表示超平面的偏置或者截距；
  • 点到超平面距离：根据几何知识x0到f(X)的距离可以表示如下，分子是x0带 入f(X)求绝对值，分母是法向量的二范数。 \[L=\frac{|f(x_{0})|}{||W||}\]
  • 损失函数：又叫代价函数也叫错误函数

4.8.2 感知机

感知机（perceptron）是一种二类分类的线性分类模型，也就是说，使用于将数据分 成两类的，并且数据要线性可分的情况。线性可分是指存在一个超平面能够将空间分 成两部分，每一部分为一类，感知机的目的就在于找这样的一个超平面。 假设输入数据形式为\(x=(x_{1},x_{2}....x_{n})\),即所谓的特征向量。y代表输入 数据的类别，为{+1，-1}，感知机的形式为 \[(f(x)=sign(w*x+b)\]

  • 当w*x+b>=0时，f(x)=+1;
  • 当w*x+b<0时，f(x)=-1;

f(x)就是我们对输入数据的分类，感知机的目的就在于找到合适的w和b，使得f(x)能 正确分类。w是和x维数相同的向量（一个是行向量，一个是列向量），w是我们求的超 平面的法向量，b是超平面的截距。
定义损失函数：误分类点到超平面的总距离（不定成误分类的点的个数是因为这样损 失函数对w,b不是连续可导，不易优化），假设误分类点为0，那么总距离为0. 空间中 任意一点到超平面的距离为|w*x+b|/(||w||),我们只要使得分子部分变成0就行。 对 于误分类点\((x_{i},y_{i})\)来说，如果 \(w*x_{i}+b>=0\),本应该为+1，但是误分类的话\(y_{i}=-1\),如果 \(w*x_{i}+b<0\),本应该为-1，但是误分类的话\(y_{i}=+1\),这样我们就能得到 \(-y_{i}(w*x_{i}+b)>0\),即我们可以使对误分类点的\(-y_{i}(w*x_{i}+b)\)求和， 使之最小化，当然这里是指变成0. 感知机算法的原始形式: 

//给定线性可分的数据集S和学习率e
w_{0}=0; 
b_{0}=0; 
k = 0; 
R = max_{1<=i<=l}||x_{i}||
while(1)
{
    for i = 1 to l
    if y_{i}(<w_{k}*x_{i}>+b_{k})<=0 then
        w_{k+1}=w_{k}+e*y_{i}*x_{i}
        b_{k+1}=b_{k}+e*y_{i}*R^{2}
        k=k+1
    end if
    end for
//直到在for循环中没有错误发生
//返回(w_{k}, b_{k})，这里k是错误次数
}

5 算法实现

5.1 基于加速度数据计算速度算法

5.1.1 数据源

基础数据来源于加速度数据，具体要求如下

  • X轴正方向指向脚尖，
  • X轴正负16G范围；
  • X轴数据6点均值滤波；

5.1.2 速度算法原理

# 在跑步时，X轴加速度数据呈现类正弦波波形，波峰为脚往前脚迈刚接触到大地的时刻， 波谷为脚往后蹬刚离开大地时刻，两个波峰之间的数据刚好是脚迈出1步的数据。通过 提取一个正弦波数据中的特征\(X\)，并经过线性回归分析，得出速度和特征之间的函 数关系\(V(X)\)，经过训练集数据的训练得出权重W和截距B，如果有新的特征\(X\) 时，经过\(V(X)\)计算得出速度值。1步内特征包含

  1. 加速度数据的均值；
  2. 加速度数据的标准差；
  3. 功率：加速度平方/(n*1000);

5.1.3 距离算法原理

通过速度算法计算出1个正弦波速度V，在计算1个正弦波的时间T，1个正弦波的距离l 通过公式可以计算出1步的距离。通过总的步数N可以计算出总的距离\(L=N*l\)。 \[l=V*T\]

5.1.4 着地时间算法原理

通过速度算法原理中描述的跑步过程，可知，1步的着地时间，可以通过计算波峰和 波谷之间的时间来估算，总的着地时间即为步数乘以1步的着地时间。

5.1.5 冲刺次数算法原理

基于速度算法原理输出的速度参数，统计在一定时间t内，速度递增v，表示一次冲刺， 目前t阈值设置为5秒，v设置为1m/s，步骤如下；

  1. 缓存t时间内的速度输出n个；
  2. 校验n个v是否递增，如果不递增清空缓存，否则进到第三步；
  3. 以第n个v减去第1个v，如果相差1m/s，则判断为1次冲刺；
  4. 清空缓存，重复第1到第4步；

Author: 比克曼

Email: bitman@163.com

Created: 2020-06-05 周五 00:04

Validate